Techniques
Level 1: Beginner
An Open Single is the easiest clue to spot. Whenever any row, column, or block has 8 numbers filled in, the ninth is an Open Single. Simply fill in the last cell with the missing number. In the example below, the yellow cell must be an 8.

A Naked Single is when an empty cell has only one possible value — all the other eight values have been eliminated as candidates — usually because they appear elsewhere in that cell's row, column, or block. In the example below, the yellow cell has a naked single on the number 4. It is the only possibility for the cell. Naked singles can be hard to spot without pencil marks.
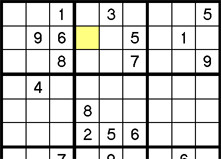
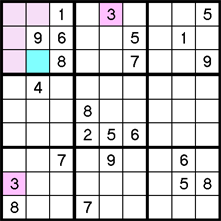
A Hidden Single is when an empty cell is the only cell in a given row, column, or block, that can possibly contain a given value — because the rest of the cells in that "house" are eliminated by neighboring cells. Hidden Singles in blocks are often somewhat easy to spot without pencil marks. In the left example below, the blue cell is the only cell in the upper left block that can be a 3. The other 4 cells are eliminated by neighboring 3's. The right example is the exact same puzzle, but with pencil marks. Notice the yellow cell is the only cell in the block containing a 3 as a pencil mark - the 3 is "hidden". Either method will help you find Hidden Singles.
Level 2: Intermediate
When two cells in the same row, column, or block contain exactly 2 candidates, and they are the same 2 candidates, then it can be assumed that one of the cells contains one of the values, and the other cell contains the other value. Without knowing which is which, we can still be sure that all other cells in that house do NOT contain either of those values. In the example below, the blue cells only contain 1 & 9. We can remove the pencil marks "9" from the pink cells.

An Omission can take on many forms, as well as many names. Sometimes referred to as an "Intersection", "Pointing", "Blocking", or "Claiming", an Omission exploits the fact that multiple cells can be in multiple houses at the same time (a house refers to any row, column, or block). If all the possibilities for a certain value in any given house also happen to all be within a second house, then we may be able to "omit" some candidates (pencil marks) from other cells.
In the example below, take a look at the center block. Note that the two possible places in this block that can be a 6 are the blue cells. Since every block must have a 6, we can conclude that one of those blue cells must be a 6. Now let's look a little broader. Note that the two blue cells also both fall into the same row. Since we already know that one of them is a 6, and a row can only contain one 6, we can conclude that all other possible 6s in that row are not really possible. By this logic, we can remove the 6 pencil mark from all of the pink cells.
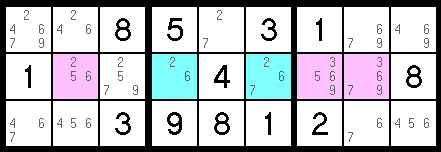
Now let's apply that same type of logic in reverse:
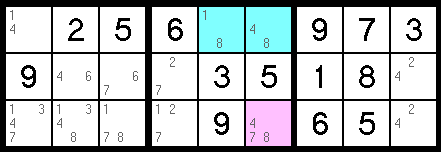
In the above example, all of the possible places for an 8 in the top row happen to also fall into the same block. Because every row must have an 8, one of the blue cells must be 8. therefore, the 8 pencil mark can be removed from the pink cell.
This same logic can be applied to the relationship between columns and blocks. Note: Omissions always involve a block and either a row or column. They cannot occur between a row and a column.
A Naked Triplet is much like a Naked Pair, except it involves three cells and three values. If three cells in the same row, column, or block all collectively contain only 3 different pencil marks, then those three cells must contain those three values, and without knowing which contains which, we can still safely eliminate them as candidates for the other cells in that "house". In the example below, the three blue cells all only contain the pencil marks 1, 2, and 8. Since they are all in the same row, they must all contain different values, so we can logically assume that one of them is the 1, one is the 2, and one is the 8. Because of this, we can safely remove any 1, 2, or 8 from all of the pink cells.
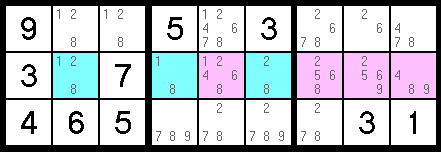
Level 3: Expert
A Hidden Pair is when two cells in the same row, column, or block, are the only two in that "house" to contain two particular values. Unlike the Naked Pair rule, which omits pencil marks from other cells, this rule omits pencil marks from the cells themselves. Since the two cells are the only ones to contain the two values, it can be assumed that one of the cells contains one of the values, and the other cell contains the other value. Without knowing which is which, we can still be sure that none of the other pencil marks are valid candidates. In the example below, the blue cells are the only two in the block that contain 4 & 9. We can remove the pencil marks 1, 7, & 8 from them.
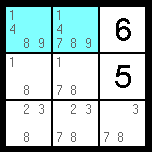
A Naked Quad is much like a Naked Pair Triplet, except it involves four cells and four values (in addition to being much more rare). If four cells in the same row, column, or block all collectively contain only 4 different pencil marks, then those four cells must contain those four values, and without knowing which contains which, we can still safely eliminate them as candidates for the other cells in that "house". In the example below, the four blue cells all only contain the pencil marks 4, 5, 7, & 8. Since they are all in the same row, they must all contain different values. Because of this, we can logically assume that one of them is the 4, one is the 5, one is the 7, and one is the 8. We can remove any 4, 5, 7, or 8 from the rest of the row.

A Hidden Triplet is when three cells in the same row, column, or block, are the only three in that "house" to contain three particular values. Unlike the Naked Triplet rule, which omits pencil marks from other cells, this rule omits pencil marks from the cells themselves. Since the three cells are the only ones to contain the three values, it can be assumed that each of the cells contains one of the values. Without knowing which is which, we can still be sure that none of the other pencil marks are valid candidates. In the example below, the blue cells are the only three in the block that contain 1, 3, & 6. We can remove the pencil marks 2, 4, & 5 from them.
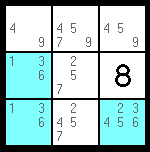
Level 4: Pro
A Hidden Quad is very hard to spot. Fortunately, it is very rare. It occurs when four cells in the same row, column, or block, are the only four in that "house" to contain four particular values. Unlike the Naked Quad rule, which omits pencil marks from other cells, this rule omits pencil marks from the cells themselves. Since the four cells are the only ones to contain the four values, it can be assumed that each of the cells contains one of the values. Without knowing which is which, we can still be sure that none of the other pencil marks are valid candidates. In the example below, the blue cells are the only four in the block that contain 5, 6, 7, & 8. We can remove the pencil marks 2 & 3 from them.
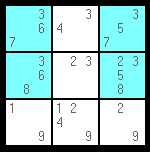
There is a mathematical principal called "Bivalue Universal Grave" (B.U.G.), which states that if each unsolved value in every row, column, and block has only two possible positions left, the puzzle will not have just one solution (and therefore it will be invalid). What this boils down to, basically, is that you cannot end up with every cell having only two pencil marks left in it. If this were to happen, the puzzle would not have been valid to begin with.
You can use this rule whenever you are at a point where every unsolved cell but one has only two pencil marks left in it. In the example below, the blue cell is the only cell left with more than two pencil marks. If we study further, we can see that removing the 2 from that cell would leave all cells with only two pencil marks (a B.U.G.). If we assume we are working on a puzzle that was valid to start out with (there is no point in assuming otherwise), then we can be sure that the blue cell must actually be a 2 in order to avoid this.
While the reason behind it is quite advanced, a B.U.G. Type 1 is very easy to spot, which is why this technique is rated as low as it is.
An X Wing involves finding two rows or columns where a given value only appears twice - and in the same two possible positions. In the example below, the two rows marked by the blue lines only have two possible positions for the number 2, and they happen to be in the same columns. Because the pencil marks say the 2's in the blue rows must be in the red columns, it follows that the 2's in the red columns can only be in one of the blue rows — one in the upper blue row and one in the lower. Regardless of which is which, we can be sure that any 2 in the red columns that is not in a blue cell is invalid. The pink cells cannot be 2 and those pencil marks can be removed.
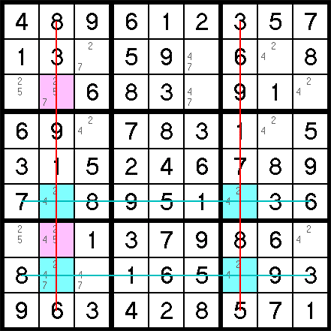
A Swordfish is just like an X Wing, except it involves three rows or columns sharing three positions for the same value. In the example below, the three rows marked by the blue lines all have only two or three possible positions for the number 5, and they all happen to be in the same three columns. Because the pencil marks say the 5's in the blue rows must be in the red columns, it follows that the 5's in the red columns can only be in the blue rows — one in each. Regardless of which is which, we can be sure that any 5 in the red columns that is not in a blue cell is invalid. The pink cells cannot be 5 and those pencil marks can be removed.
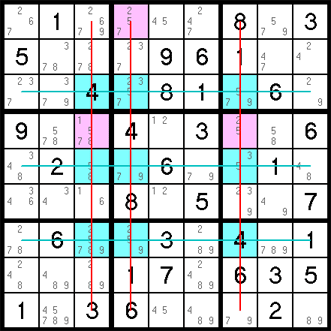
The Unique Rectangle rule uses the same type of logic as the B.U.G. rule (above) - it assumes the puzzle you are working on is a valid one. The rule states that if the same two pencil marks appear in four separate cells, and these cells fall into exactly two rows, columns, and blocks, then it will create a B.U.G., meaning the puzzle was invalid to begin with. In simple terms, you can't have four cells forming a square with the same 2 pencil marks in them, so long as those four cells fall into only two blocks.
As with a B.U.G., this is a complex concept, but quite easy to spot. In the example below, if the numbers 6 & 8 were removed from the yellow cell, the puzzle would end up with two possible solutions — with the 4's and 5's alternating diagonal from each other. We can assume the puzzle has only one solution (or we wouldn't be working on it in the first place), so we can safely remove both the 4 and the 5 from the yellow square.

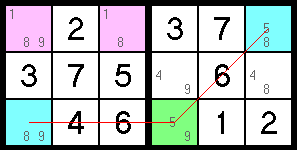
An XY Wing (sometimes just called "Y Wing") involves finding three different cells with only two pencil marks each, that collectively contain only three different pencil marks. If these cells are not all in the same row, column, or block, but one of them shares a relationship with both of the other two, then together the three can create an exclusion rule. In the example below, the green cell and the two blue cells each have only two pencil marks and together share only three different values — 5, 9 & 8. Because the green cell shares a row, column, or block with each of the blue cells, this creates an XY Wing on the number 8 — no matter what the final solution to the green cell is, one of the two blue cells will be 8. Because we know this, we can be sure that any cell that intersects both of the blue cells cannot be 8. The 8 pencil mark can be removed from both of the pink cells.
Level 5: Master
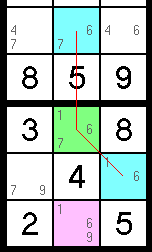
An XYZ Wing is an XY Wing (above) taken one step further. While it still involves three cells encompassing only three different pencil marks, they don't all have just 2 pencil marks — one of them has three — but the exclusion still works. In the example below, the green cell can only be 1, 6, or 7. If it is 1 or 7, then one of the blue cells has to be 6, because they share a relationship with the green cell. No matter what happens, one of the two blue cells or the green cell itself will end up being 6. Because of this, any cell that intersects all three cells - the green cell and the two blue cells — cannot be 6. The 6 pencil mark can be removed from the pink cell.
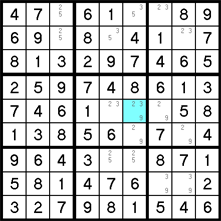
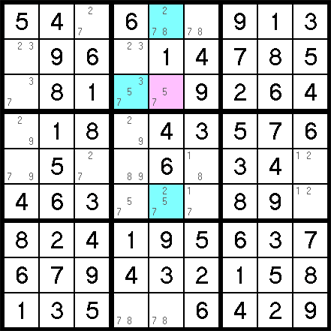
There is a mathematical principal called "Bivalue Universal Grave" (B.U.G.), which states that if each unsolved value in every row, column, and block has only two possible positions left, the puzzle will not have just one solution (and therefore it will be invalid). What this boils down to, basically, is that you cannot end up with every cell having only two pencil marks left in it. If this were to happen, the puzzle would not have been valid to begin with.
Unlike a B.U.G. Type 1, this Type 2 is much harder to spot. Remember, what we are trying to avoid is the impossibility of having two pencil marks left in every cell. In the example below, note there are only three cells with more than two pencil marks (highlighted in blue). Also note they all contain a 7. And finally, note that if the 7 were removed from all of them, we would not be given any new singles or pairs, etc, and we would be stuck with all cells with only 2 pencil marks — which as previously stated cannot happen. Therefore, we can assume in this situation that one of the blue cells must be a 7. And although we do not know which, we do know that any cell that intersects all three of them cannot be 7. The 7 pencil mark can be removed from the pink cell.
When no other techniques are left, we must resort to Forcing Chains. "Forcing Chain" is a term that refers to finding a hypothetical impossibility among the pencil marks that are left, and subsequently ruling out that pencil mark. Assuming the puzzle is valid and has only one solution, then only one of the pencil marks left in every unsolved cell can be the right one — the rest must be wrong. A Forcing Chain is merely a proof that one of them is wrong by pointing out events that lead to an "impossibility". Examples of an impossibility include a cell left with no more pencil marks, two cells in the same house that have the same single pencil mark, or an entire house with no possible place for a given number.
Type 1 is the simplest type of Forcing Chain (while still very complex in comparison to other Sudoku solving techniques), involving no more than two steps to an impossibility, and using the same value in both steps.
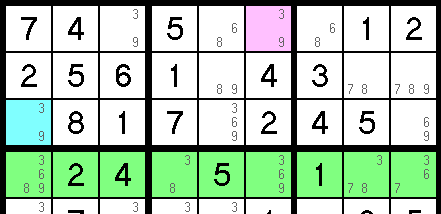
In the example below, we will prove that the pink cell cannot be a 9. We will do this by looking at what would happen if it were a 9. If the pink cell were a 9, it would remove all the other 9's in its row, thereby forcing the blue cell to also be a 9. When the pink and blue cells are both 9, note that the entire green row no longer has a place for a 9, which is not possible. We can conclude that the pink cell cannot be 9, and that pencil mark can be removed.
Tip: When looking for forcing chains, start with the cells that have only two pencil marks. If you can disprove one of those pencil marks first, you can solve the cell!
When no other techniques are left, we must resort to Forcing Chains. "Forcing Chain" is a term that refers to finding a hypothetical impossibility among the pencil marks that are left, and subsequently ruling out that pencil mark. Assuming the puzzle is valid and has only one solution, then only one of the pencil marks left in every unsolved cell can be the right one — the rest must be wrong. A Forcing Chain is merely a proof that one of them is wrong by pointing out events that lead to an "impossibility". Examples of an impossibility include a cell left with no more pencil marks, two cells in the same house that have the same single pencil mark, or an entire house with no possible place for a given number.
Type 2 is a step up in complexity from Type 1. It can involve up to three steps to an impossibility, and does not necessarily use the same number in each step.
In the example below, we will prove that the pink cell cannot be a 2. We will do this by looking at what would happen if it were a 2. If the pink cell were a 2, it would force the blue cell to be a 4, because it would be the only 4 left in the row. This would cause the orange cell to be an 8, because it would be the only 8 left in the row. With the blue cell being a 4, and the orange cell being an 8, the entire block above them (highlighted in green) would now have two open cells whose only candidate is a 7. Since they cannot both be a 7, we have created an impossibility, and proven that the pink cell cannot be a 2. That pencil mark can be removed.
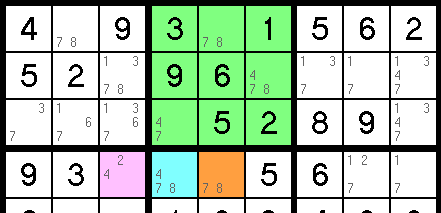
Tip: When looking for forcing chains, start with the cells that have only two pencil marks. If you can disprove one of those pencil marks first, you can solve the cell!
Level 6: Genius
When no other techniques are left, we must resort to Forcing Chains. "Forcing Chain" is a term that refers to finding a hypothetical impossibility among the pencil marks that are left, and subsequently ruling out that pencil mark. Assuming the puzzle is valid and has only one solution, then only one of the pencil marks left in every unsolved cell can be the right one — the rest must be wrong. A Forcing Chain is merely a proof that one of them is wrong by pointing out events that lead to an "impossibility". Examples of an impossibility include a cell left with no more pencil marks, two cells in the same house that have the same single pencil mark, or an entire house with no possible place for a given number.
Type 3 Forcing Chains, also referred to as "Complex Forcing Chains," require four or more steps to prove an impossibility. Puzzles that require this type of Forcing Chain are the most diabolical and by far the hardest to solve. Theoretically, though, all valid puzzles can eventually be solved with them.